Aha! Develop is for healthy enterprise development teams — that use scrum, kanban, and SAFe frameworks


Learn more
Toray Altas · 2020-06-29 · quantum, development, cloud

Quantum computing in the real world

Why does it matter?

As we have recently entered a new decade, I have been thinking about the next leaps in computer science and where some of those areas may be. One such area that I have read a lot about in passing but never really explored is quantum computing. I believe quantum computing may become very important in the future, as it will provide us with an opportunity to do parallel computing in ways that have never been possible before with classical computers. Such areas include:

  • Cryptography - Encryption and SSL may fundamentally change and allow for true "randomisation" when it comes to key generation. This will perhaps have the most impact on software organisations like Aha!
  • Molecular analysis - with the current pandemic, we have seen a rapid rise in popularity of such projects as the "Folding at home" where analysis of the coronavirus protein movements are done using a volunteer distributed computing model. This could be done in a much more efficient way using quantum computing not only for the current virus, but many molecular components and interactions such as new pharmaceutical drugs in humans.
  • Optimisation - imagine running a large airline where you have multiple variables in determining the most efficient way to use your resources (planes, routes, pilots, etc). Currently this is difficult and complicated to calculate using conventional computers, these kinds of optimisation problems are what some quantum computers thrive at.

Annealing vs gate

There are currently two types of quantum computers in production: annealing quantum computers and gate based quantum computers. Annealing computers are generally used for specific types of optimisation problems, while gate based computers aim to be a more universal computer that can solve a multitude of problem types. This article aims to cover gate-based quantum computers given their universality.

Superposition and entanglement

In order to understand how a gate-based quantum computer works, we need to understand two principles of quantum physics: superposition and entanglement.

Superposition — In classical computers we always know that a bit is either a 0 or 1. Anything else is simply an error state. However in quantum computers, using the principle of superposition, a quantum bit (qubit), can both be a 0 and 1 at the same time. When we "observe" a qubit as a classical bit, it collapses back to a 0 or a 1 based on a probabilistic model.

Entanglement — This is a more complicated principle in quantum computing and can be the most difficult to conceptualise. When we have two qubits that are in superposition (i.e. the qubits represent the states 00, 01, 10, and 11 at the same time), and we collide the two qubits together, upon collapsing one of the qubits to its classical state, we know what the outcome of the other non collapsed qubit will be when we collapse it. So the two qubits are correlated, upon entangling them together. An example further down in this article will help explain this further.

Quantum computing gates

Quantum 101

Going back to your 101 computer science class, in a classical computer, we represent a classical "bit" as a scalar number, a 0 or a 1. In a quantum computer, we represent a "qubit" (quantum bit) as a vector:

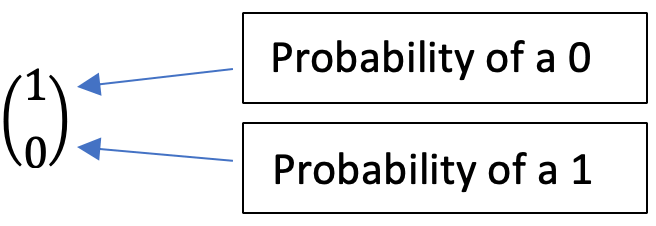
0 qubit

In this image, we see a 0 qubit, as the top number in the vector represents the probability of a 0 after classical bit measurement. So there is a 1 representing a 100% chance of observing a "0" bit upon measuring with a classical bit. Conversely, the bottom number in the vector represents the chance of seeing a 1 bit upon observing the qubit. It has a 0 probability.

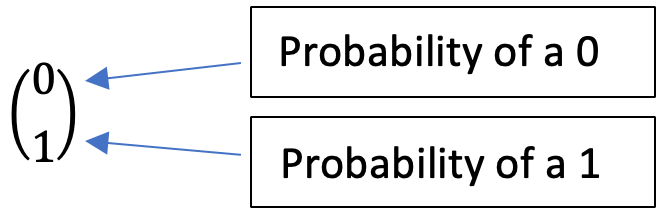
1 qubit

This is the same with a 1 qubit, but in reverse, where we see that the bottom number in the vector represents the probability of a 1 after classical bit measurement, with a 100% chance of observing a 1 and 0% chance of observing a 0.

Very simple, right? Just like in classical computing, these qubits become interesting when you start applying gate logic to them. In classical computers we use scalar boolean algebra to determine the output based on the input. In quantum computing we need to use matrix algebra to determine the output based on the input. The advantage of using matrix algebra over scalar algebra, is that we are able to parallelise out computations over multiple inputs/outputs rather than just a single input/output.

Let's look at a "not gate":

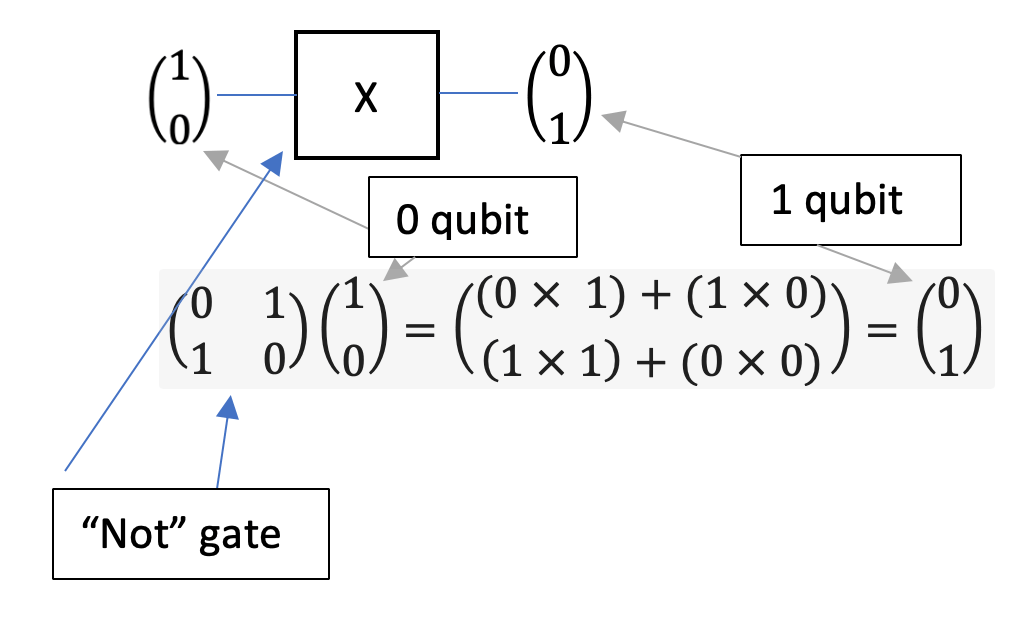
Not gate

In this diagram, we can see the dot product of a not gate matrix with a 0 qubit vector produces a 1 qubit vector upon evaluation (the reverse being true for a not on a 1 qubit vector).

This is a simple example of how gates work in quantum computing. However things begin to get more interesting when we do not have a 100% probabilistic outcome of a 0 or 1.

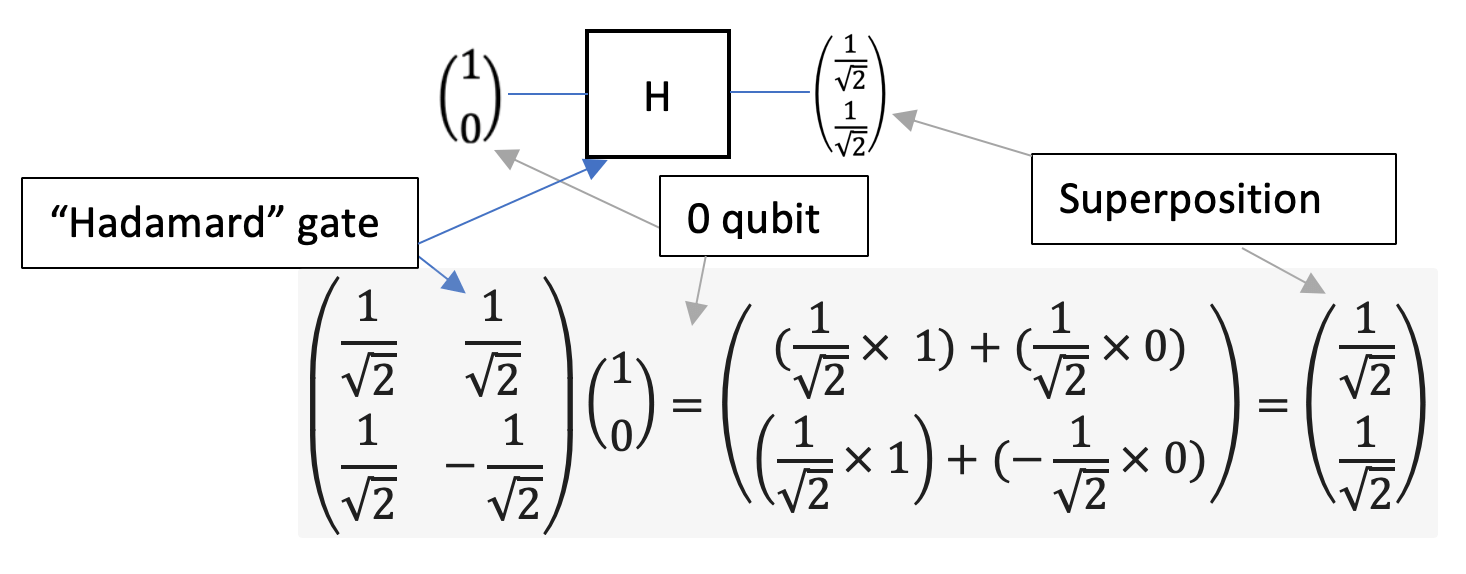
Hadamard gate

This is a Hadamard gate — upon applying this to a 0 qubit, we get this strange result in the vector with non-integer numbers. What does this mean?

As earlier explained, the top number in a qubit vector represents the probability of a 0, and second the probability of a 1. What I didn't say for simplicity's sake, was that you need to square the probabilistic value in order to determine its probability. So in the results of the Hadamard gate being applied to a 0 qubit, there is a 50% chance of 0 and a 50% chance of a 1. This is called superposition, as the qubit is both a 0 and 1 until observed in the classical world!

Representation of bits

As seen, we can represent a single quantum as a vector, but how do we represent multiple bits?

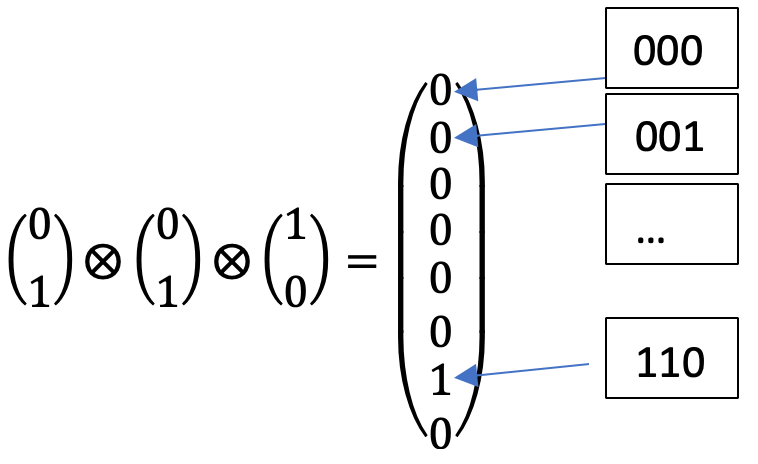
Tensor multiple bits

We can display them mathematically as vectors being tensor multiplied. We can see here a 110 being represented as a single vector after being tensor multiplied together. You can observe that the probabilistic model still holds for a single vector that is longer than just 2. The top number represents the probability of a 000, second number a 001, third number 010, etc until we get to the second last number which represents a 110 with 100% chance (from the 1).

This is important if we want to understand an entanglement circuit:

Entanglement circuit

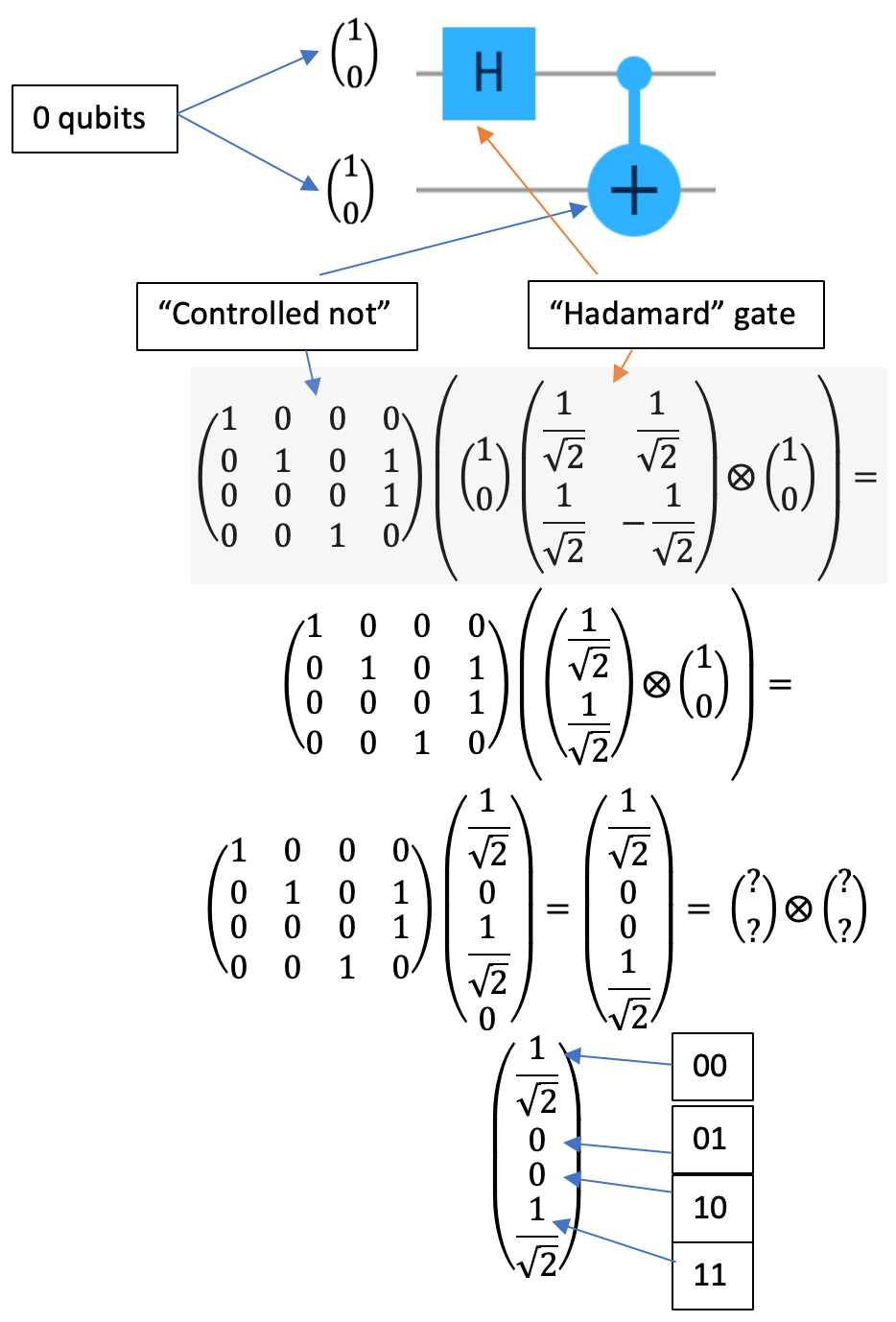
The initial state for our two qubit is 0 each (represented by the tensor product). We then apply a Hadamard gate to put one of the gates into superposition, followed by actually calculating the tensor product so we get a vector with length 4. We then apply a special gate called a "controlled not gate", represented by the 4x4 matrix. Which lands at a slightly modified vector with length 4.

Now if we try to factor that vector of length 4 to be 2 vectors of length 2 each, i.e. represent the results as 2 qubits, we find we actually mathematically can't. It’s kind of like trying to refactor the prime number 13 into its factors. If we look at the probabilities of this single vector of length 4, we observe that we have a 50% chance of observing a 00 and a 50% chance of observing a 11 if we collapse the qubits state back to the classical world. So we can confidently say, if we observe one qubit in the classical world, and it turns out to be 0, then it follows that we immediately know that the other qubit will also collapse to 0. Conversely, if we observe one qubit in the classical world, and it turns out to be 1, then it follows that we immediately know that the other qubit will also collapse to 1.

Congratulations, you have now mathematically shown the entanglement principle of quantum mechanics that we mentioned earlier!

The real world

We can actually run this circuit on a real quantum computer using IBM's cloud quantum computing platform:

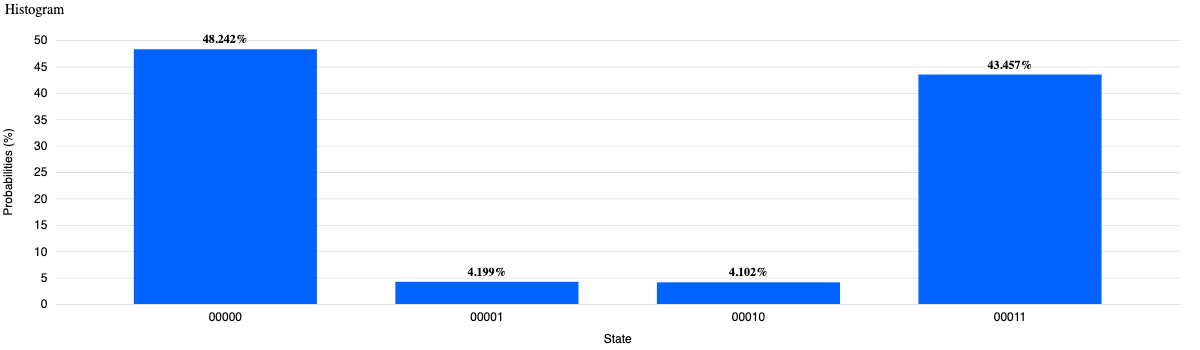
IBM quantum experience

However, what we observe is that it isn't quite 100% of the time 00 or 11. There is some noise! This is because in the real world, quantum computers are delicate machines highly sensitive to outside interference. This is why if we run this circuit 1000 times, we see that sometimes it can stray from what the theoretical results can be, just like silicon in a classical computer can have errors due to physical imperfections. At the time of this writing, there are some limitations in quantum computers that are available. Most quantum computers today do not have many bits available to use due to the high error rate with each additional bit made available, so it makes it impractical for some of the uses we talked about earlier.

That said, one of the most talked-about algorithms where quantum computing will end up being used— is Shor's algorithm:

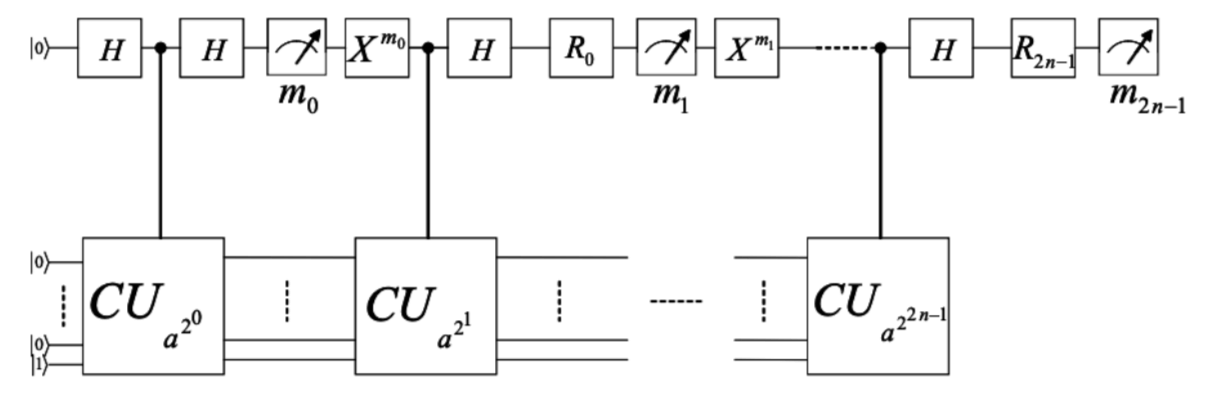
Part of Shor's algorithm

A quantum computer using Shor's algorithm can break down a RSA-2048 bit encryption key in 10 seconds, where a classical computer would take 30+ million years to do it. This would fundamentally change the way we use the internet and how to encrypt our sensitive data. Luckily, there are countermeasures to this with quantum encryption methods. It is also somewhat moot, as we need a 4000 bit quantum computer that has a low error rate, and at the moment, the quantum computer with the most bits has about 100. Many people are trying to project when we will get a 4000 bit quantum computer, but it's hard to be a Nostradamus when the industry is in its infancy.

Given all this, I think it's prudent for us to keep an eye on developments in this field and to understand the advantages and disadvantages of quantum computing as a whole.

References

Toray Altas

Toray Altas

Toray enjoys learning about new engineering problems and figuring out the best way to solve them. He is a senior software engineer at Aha! — the world’s #1 product development software. He has worked on many of the features in Aha! that you know and love.

Build what matters. Try Aha! free for 30 days.

Follow Aha!

Follow Toray